Binary Space Partitioning
Binary Space Partitioning is an algorithim that takes a set of 2D lines or 3D polygons and recursively groups them into a BSP Tree. Each node has three lists: two child nodes representing lines in front of and lines behind and a thirt list representing lines on the same plane. Once the BSP Tree is built it can be used to search which lines are facing any position in linear time.
It originally was created in 1969 during early attempts at 3D rendering but was most popularly introduced by John Carmack in the original DOOM game. In the game, a level editor was used by the DOOM team to create levels which were comprised by sectors and line data called linedefs. When publishing their level data, Binary Space Partitioning was run against the level and produced a BSP tree of LineDefs and subsplit linedefs called Segs. This BSP tree was then included in their level data for the game engine called a WAD file.
When the DOOM engine loaded the data from the level, it would use the BSP tree nodes to traverse and render the game in a reverse painters algorithm. The BSP tree allowed the game engine to only search and draw walls that were facing the player, culling large numbers of walls from the process. This was where the BSP shined allowing DOOM to run in ways other DOS games had not at the time.
A BSP tree is computationally expensive to run, which is why it was done during level creation and as such required levels be static in nature without horizontal changes in the map's layout.
The Algorithm
- Two connected vertices define a LineDef
- A LineDef has an outward face to define which side of it is considered open and which side is solid
- A list of LineDefs form a Polygon that can define the boundaries of a room, or "sector"
- A Binary Space Partition class accepts the worlds list of LineDefs
- The BSP chooses a best candidate "splitter" LineDef by which to judge all other LineDefs
- The BSP creates two child BSPs to place other LineDefs behind or in front of the splitter
- LineDefs that cross the plane of the splitter and split into smaller LineDefs to be sorted
- The BSP sorts all LineDefs recursively in the child trees
- Using the BSP we can test whether a position is in open space with a depth search
- Using the BSP we can also render all walls from either back to front or front to back
- Doom rendered them front to back and used culling to prevent overdraw
- Other engines have rendered back to front called the Painters Algorithm
- The BSP Tree is built before the game begins as a means of significant performance gain
Creating 2D Rooms of Connected Lines
Using Python I will demonstrate how a BSP is built, but first we need to create some meaningful polygons to split into a BSP tree. This set of polygons will be comprised of lines with: x coord, y coord, which way it is "facing", and the height of the wakll (used only in rendering).
NOTE: all math is included at the end.
# Lines, each vertex connects to the next one in CW fashion
# third element is direction its facing, when CW facing 1 = left
polygons = [
# open room
[
# x, y, facing, height
[30, 30, 0, 10],
[300, 20, 0, 10],
[400, 300, 0, 10],
[30, 200, 0, 10]
],
# inner col
[
# x, y, facing
[50, 50, 1, 5],
[100, 50, 1, 5],
[75, 75, 1, 5],
[100, 100, 1, 5],
[50, 100, 1, 5]
],
# inner room
[
[55, 55, 0, 5],
[70, 55, 0, 5],
[70, 95, 0, 5],
[55, 95, 0, 5],
]
]
# Line Defs built Clockwise
allLineDefs = []
for i, v in enumerate(polygons):
polygon = polygons[i]
lineDefs = []
for idx, val in enumerate(polygon):
lineDef = LineDef()
# first point, connect to second point
if idx == 0:
lineDef.asRoot(polygon[idx][0], polygon[idx][1], polygon[idx + 1][0], polygon[idx + 1][1], polygon[idx + 1][2], polygon[idx + 1][3])
lineDefs.append(lineDef)
allLineDefs.append(lineDef)
# some point in the middle
elif idx < len(polygon) - 1:
lineDef.asChild(lineDefs[-1], polygon[idx + 1][0], polygon[idx + 1][1], polygon[idx + 1][2], polygon[idx + 1][3])
lineDefs.append(lineDef)
allLineDefs.append(lineDef)
# final point, final line, connects back to first point
elif idx == len(polygon) - 1:
lineDef.asLeaf(lineDefs[-1], lineDefs[0], polygon[idx][2], polygon[idx][3])
lineDefs.append(lineDef)
allLineDefs.append(lineDef)These polygons contain line data which are similar to LineDefs in DOOM, and of note the have a "face" direction which indicates which side is the exposed side to the game world and should be rendered. This facilitates the concept of a wall and is important for subdividing the other lines into the BSP tree.
These polygons when glued together and rendered look like this, with a larger room in which our world is contained and within a smaller room completely enclosed within another set of walls.
The blue lines are the overall walls, the smaller lines projecting as their normal vector represent their face's direction. The Dot and Line are the camera position and angle in the 2D world.
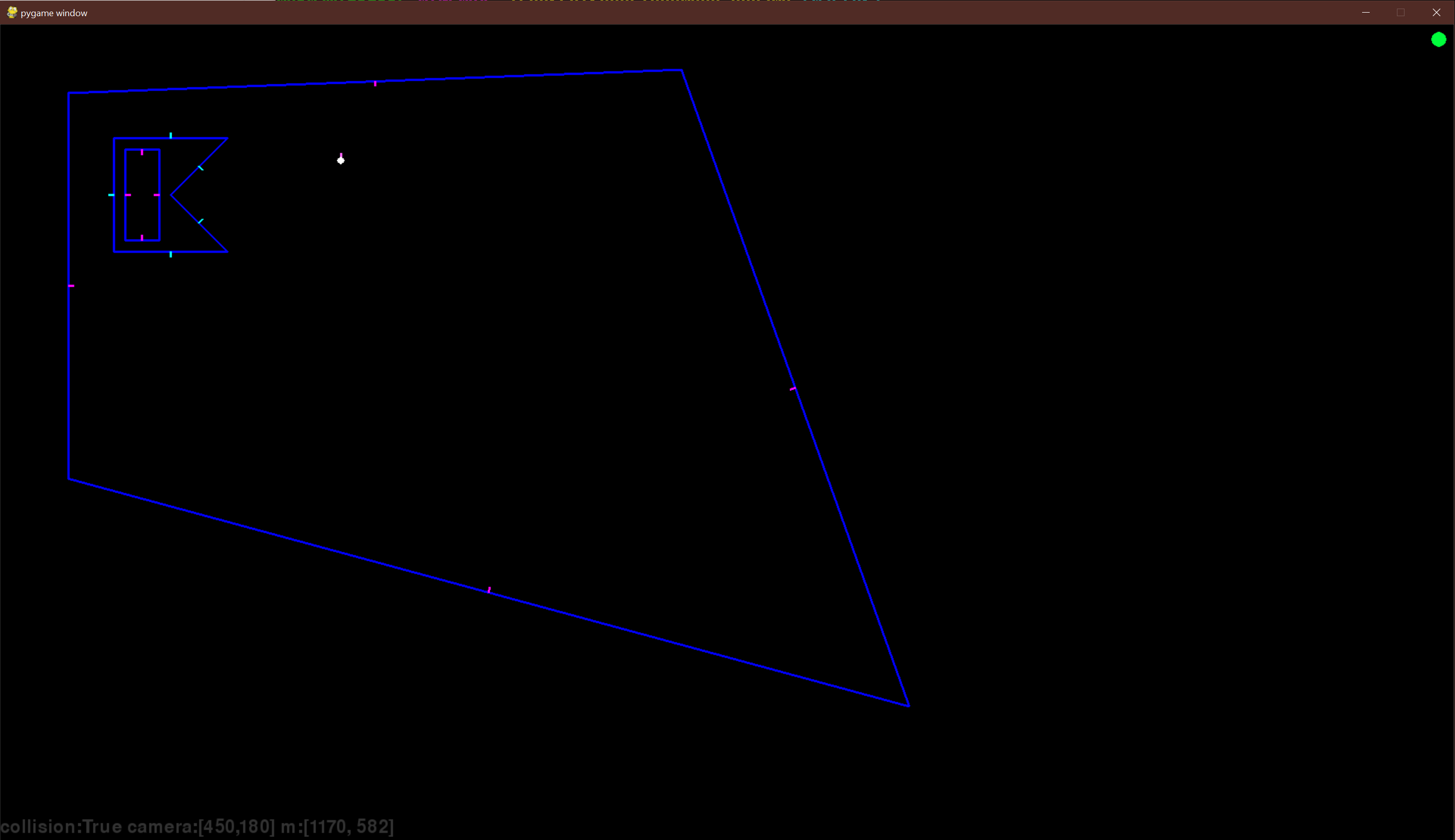
This algorithm converts the raw polygon data into a LineDef object that is defined as:
import random
from engine.mathdef import crossProductLine
from engine.mathdef import normalize
from engine.mathdef import intersection2d
from engine.mathdef import pointBehindSegment
# A polygon is a collection of lines, each line has a direction
# All lines should be connected, meaning one should start where the last one ends
class LineDef(object):
def __init__(self):
self.start = []
self.end = []
self.facing = None
self.mid = []
self.normals = []
self.drawColor = (random.randint(10, 255), random.randint(10, 255), random.randint(50, 255))
self.height = 10
# TODO: get normals and stuff calculated here
def asRoot(self, startX, startY, endX, endY, facing, height):
self.start = [startX, startY]
self.end = [endX, endY]
self.facing = facing
self.height = height
self.setup()
def asChild(self, preLineDef, endX, endY, facing, height):
self.start = [preLineDef.end[0], preLineDef.end[1]]
self.end = [endX, endY]
self.facing = facing
self.height = height
self.setup()
def asLeaf(self, preLineDef, rootLineDef, facing, height):
self.start = [preLineDef.end[0], preLineDef.end[1]]
self.end = [rootLineDef.start[0], rootLineDef.start[1]]
self.facing = facing
self.height = height
self.setup()
def setup(self):
self.setMidpoint()
self.setNormals()
def setMidpoint(self):
# (a.x+b.x)/2,(a.y+b.y)/2
self.mid.append((self.start[0] + self.end[0]) / 2)
self.mid.append((self.start[1] + self.end[1]) / 2)
def setNormals(self):
dx = self.end[0] - self.start[0]
dy = self.end[1] - self.start[1]
self.normals.append(normalize(-dy, dx)) # First normal is the one facing in (if we are Clockwise)
self.normals.append(normalize(dy, -dx)) # Second normal is the one facing out (if we are Clockwise)
def isPointBehind(self, a, b):
# If it is behind and we are facing left CW
beh = pointBehindSegment([a, b], self.start, self.end) # true, false or none (for on the same plane)
if beh != None:
if self.facing == 1:
return beh
return not beh
return None
def classifyLine(self, testLine):
# 1 = back
# 2 = front
# 3 = spanning
# 4 = co planar
points = [testLine.start, testLine.end]
backCounter = 0
frontCounter = 0
for point in points:
result = self.isPointBehind(point[0], point[1])
if result == True:
backCounter += 1
if result == False:
frontCounter +=1
# if result == None:
# co planar, no counters
# spanning
if backCounter != 0 and frontCounter != 0:
return 3
# back
if backCounter:
return 1
# front
if frontCounter:
return 2
return 4
def split(self, other):
# get the intersecting point
intersection = self.findIntersection(other)
if intersection:
# create a line from other start to intersection and return that as front??
splitA = [other.start, intersection]
splitB = [intersection, other.end]
aBehind = self.isPointBehind(other.start[0], other.start[1])
# return them with position 0 behind and position 1 in front
if aBehind:
return [splitA, splitB]
else:
return [splitB, splitA]
return None
def findIntersection(self, other):
return intersection2d(self.start, self.end, other.start, other.end)The BSP Tree Data Structure
Here is a BSP Tree class that does all the brutal work. Being a tree the actual class is just a sindle Node of the tree with recursive functions for traversing and building child Node lists.
class SolidBSPNode(object):
def __init__(self, lineDefs):
self.splitter = None # LineDef
self.front = None # Self
self.back = None # Self
self.isLeaf = False
self.isSolid = False
if len(lineDefs) == 0: # leaf
return
# get splitter line
splitterIndex = self.selectBestSplitter(lineDefs)
self.splitter = lineDefs[splitterIndex]
# iterate the lineDefs and figure out which side of the splitter they are on
frontList = []
backList = []
for lineDef in lineDefs:
# skip splitter self check
if lineDef != self.splitter:
d = self.classifyLine(self.splitter, lineDef)
if d == 1:
# Behind
backList.append(lineDef)
elif d == 2 or d == 4:
# Front or coplanar
frontList.append(lineDef)
elif d == 3:
# Spanning
# first element is behind, second is in front
splits = self.splitLine(self.splitter, lineDef)
backList.append(splits[0])
frontList.append(splits[1])
# all lines have been split and put into front or back list
if len(frontList) == 0:
# create an empty leaf node
self.front = SolidBSPNode([])
self.front.isLeaf = True
self.front.isSolid = False
else:
# create our recursive front
self.front = SolidBSPNode(frontList)
if len(backList) == 0:
# create a solid back node
self.back = SolidBSPNode([])
self.back.isLeaf = True
self.back.isSolid = True
else:
# create our recursive back
self.back = SolidBSPNode(backList)
def splitLine(self, splitterLineDef, lineDef):
# first element is behind, second is in front, use facing from parent
splits = splitterLineDef.split(lineDef)
splitBehind = splits[0]
splitBehindDef = linedef.LineDef()
splitBehindDef.asRoot(splitBehind[0][0], splitBehind[0][1], splitBehind[1][0], splitBehind[1][1], lineDef.facing, lineDef.height)
splitFront = splits[1]
splitFrontDef = linedef.LineDef()
splitFrontDef.asRoot(splitFront[0][0], splitFront[0][1], splitFront[1][0], splitFront[1][1], lineDef.facing, lineDef.height)
return [splitBehindDef, splitFrontDef]
# if all points behind, we would put whole poly in back list
# if all points ahead, we would put whole poly in front list
# if overlap, split and put into both
def classifyLine(self, splitterLineDef, lineDef):
return splitterLineDef.classifyLine(lineDef)
def selectBestSplitter(self, lineDefs):
# compare each line to each other line
# classify where the line falls and increment number
best = 99999
splitterIndex = 0
for idxA, lineDefA, in enumerate(lineDefs):
fronts = 0
backs = 0
splits = 0
for idxB, lineDefB, in enumerate(lineDefs):
if lineDefA != lineDefB:
d = self.classifyLine(lineDefA, lineDefB)
if d == 1: #back
backs += 1
elif d == 2 or d == 4: # front or coplanar
fronts += 1
elif d == 3: # spanning
splits += 1
# make splits more costly
score = abs(fronts - backs) + (splits * 8)
if score < best:
best = score
splitterIndex = idxA
return splitterIndex
def inEmpty(self, testPoint):
# recurse the tree until we find a leaf node
if self.isLeaf:
return self.isSolid == False
beh = self.splitter.isPointBehind(testPoint[0], testPoint[1])
if beh:
return self.back.inEmpty(testPoint)
else:
return self.front.inEmpty(testPoint)
def getWallsSorted(self, posA, posB, walls, depth = 0):
if not self.isLeaf:
behind = self.splitter.isPointBehind(posA, posB)
# painter's algorithm paints back to front, (front to back recursively)
# to switch to doom algorithm (requires clipping) swap front and back orders
if behind:
self.front.getWallsSorted(posA, posB, walls, depth + 1)
# walls.append(self.splitter)
self.back.getWallsSorted(posA, posB, walls, depth + 1)
else:
self.back.getWallsSorted(posA, posB, walls, depth + 1)
walls.append(self.splitter)
self.front.getWallsSorted(posA, posB, walls, depth + 1)Hopefully the code is self explanatory in regards to the algorithm itself.
Some of the more complicated elements include determining if a LineDef plane crosses another line def plane and splitting that location.
Of note as well is the concept of if a node isSolid. This is a flag that is set for all node children that are created. All Leaf nodes do not actually contain line lists but two primay flags: isLeaf and isSolid. The parent of a leaf node is actually the parent of two leaf nodes, one in front and one behind. We can designate all "behind" leaf nodes as isSolid=true.
If we test a position against the tree and we wind up at a leaf node that isSolid we know the position is invalid.
Segs
The splitting and sorting operation creates the segs, or sub segments of lines and can be seen here as different colored lines that comprise either all or portions of our previous line defs.
Can you determine which line was the "Splitter" line of this BSP tree from the segs created?
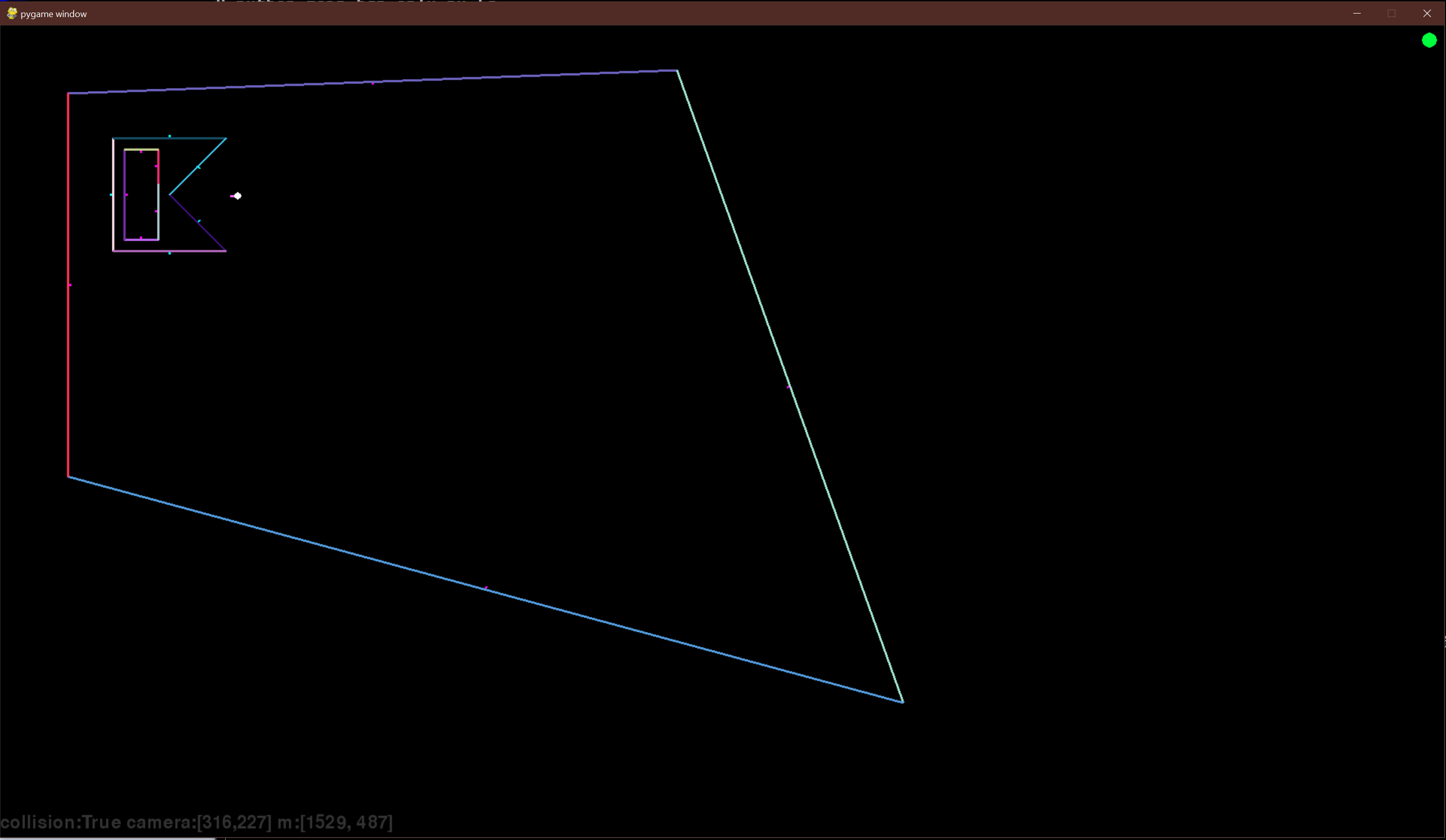
This drawing routine is appended to our BSP class such as
def drawSegs(self, display, depth = 0):
# draw self
if self.isLeaf == False:
ln = 4
mx = self.splitter.mid[0]
my = self.splitter.mid[1]
nx = self.splitter.normals[self.splitter.facing][0] * ln
ny = self.splitter.normals[self.splitter.facing][1] * ln
if self.splitter.facing == 1:
display.drawLine([ [mx, my] , [mx + nx, my + ny] ], (0, 255, 255), 1)
else:
display.drawLine([ [mx, my] , [mx + nx, my + ny] ], (255, 0, 255), 1)
display.drawLine([self.splitter.start, self.splitter.end], self.splitter.drawColor, 1)
if self.back:
self.back.drawSegs(display, depth + 1)
if self.front:
self.front.drawSegs(display, depth + 1)Faces
We can also visualize the faces of the lines and which ones face our chosen position by recursing and testing the position with the seg's face direction. The faded lines represent those facing away from the position.

posA being the x coord and posB being the y coord of the camera or player
def drawFaces(self, display, posA, posB, depth = 0):
# draw self
if self.isLeaf == False:
behind = self.splitter.isPointBehind(posA, posB)
if not behind:
display.drawLine([self.splitter.start, self.splitter.end], (255, depth * 20, 0), 1)
else:
display.drawLine([self.splitter.start, self.splitter.end], (60, depth * 5, 0), 1)
if self.back:
self.back.drawFaces(display, posA, posB, depth + 1)
if self.front:
self.front.drawFaces(display, posA, posB, depth + 1)Walls
We simply need to adjust how we are rendering our faces to not render lines facing away from the player. Traversing before or after rendering defines in which order we render our walls facing our player.
The traditional Painters Algorithm renders based on furthest to closest, each wall covering the one behind it. This is simple but non-performant as large portions of walls are rendered and then overwritten wastefully.
In DOOM they revesed the approach rendering from closest to furthest. Because the game was actually 2D projected as 3D the geometry was simple enough to keep a running list of screen coords that were rendered to and to cull any walls behind the walls already rendered.
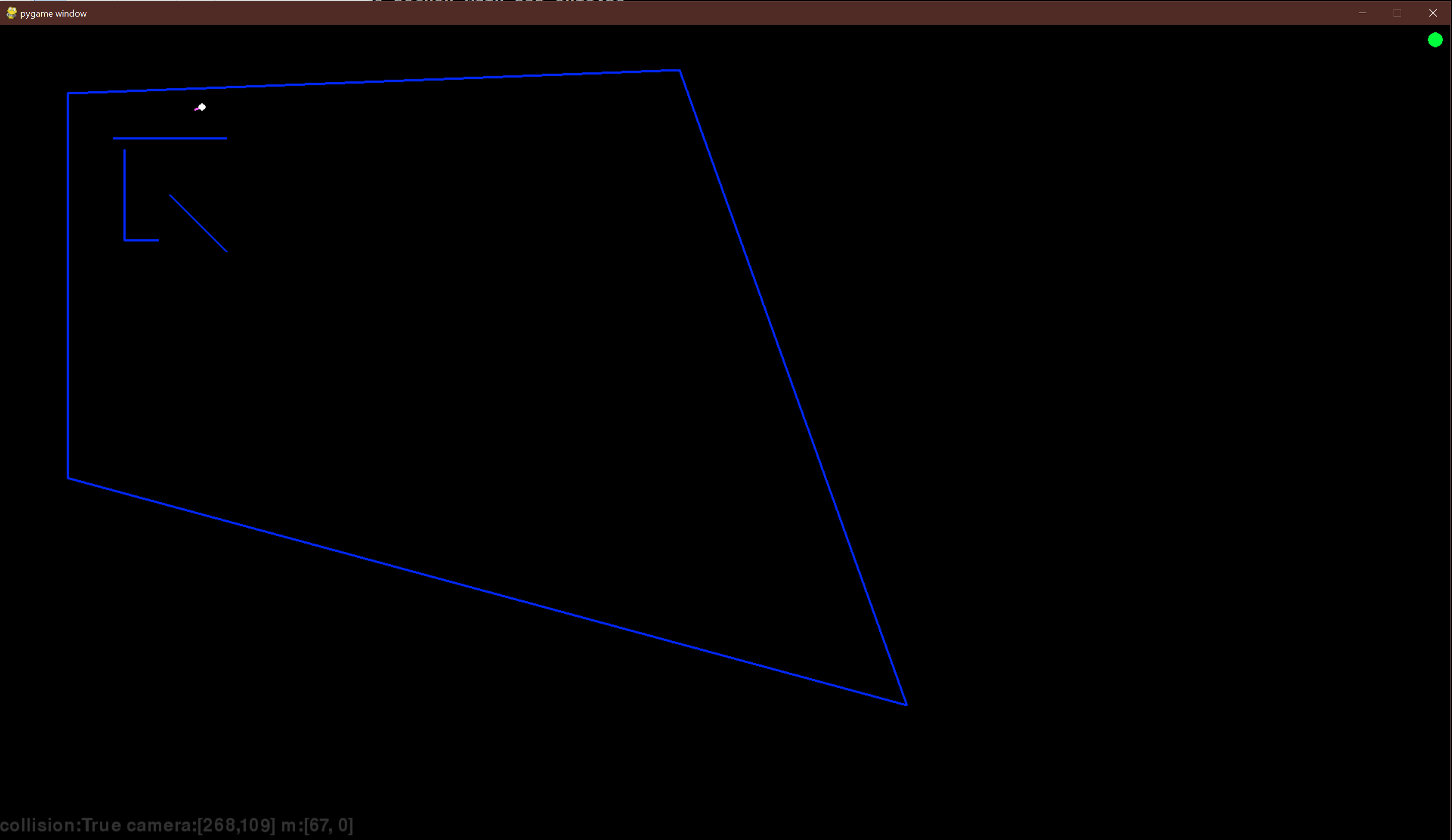
def drawWalls(self, camera, display, depth = 0):
if self.isLeaf == False:
behind = self.splitter.isPointBehind(camera.worldX, camera.worldY)
if not behind:
topLeft, topRight, bottomRight, bottomLeft = camera.projectWall(self.splitter, display.width, display.height)
if topLeft:
wallLines = [ topLeft, topRight, bottomRight, bottomLeft ]
display.drawPolygon(wallLines, self.splitter.drawColor, 0)
if self.front:
self.front.drawWalls(camera, display, depth + 1)
if self.back:
self.back.drawWalls(camera, display, depth + 1)Basic Collision/Bounds Checking
It was simple enough to test if the position is "within" a wall" through a form of BSP collision detection. Enabling this check in code prevented the player from crossing a wall.
We can facilitate this with a check to see if the leaf node of the tree we wind up in is considered solid or not. If the position we are testing is in a lead node that is solid then it is not allowed.
def inEmpty(self, testPoint):
# recurse the tree until we find a leaf node
if self.isLeaf:
return self.isSolid == False
beh = self.splitter.isPointBehind(testPoint[0], testPoint[1])
if beh:
return self.back.inEmpty(testPoint)
else:
return self.front.inEmpty(testPoint)Conclusions
The BSP tree is really an awesome algorithm and data structure in one. The selection of a splitter line can affect the performance. The wider and shallower our tree the faster our checks become, so more than one BSP could be tested for performance improvements.
You can see this BSP Tree in action in my Doom Engine recreation in Python.
Some of the code here was of course referenced from other documentation about a BSP tree.
Maths
As I stated before here is the math functions referenced in the code above
import math
def crossProductLine(a, b):
return a[0] * b[1] - a[1] * b[0]
#{ return (p.x*q.y - p.y*q.x); }
def pointBehindSegment(point, a, b):
cross = (b[0] - a[0]) * (point[1] - a[1]) - (b[1] - a[1]) * (point[0] - a[0])
if cross > 0:
return True
if cross < 0:
return False
if cross == 0:
return None
def normalize(a, b):
if a != 0 or b != 0:
length = math.sqrt(a * a + b * b)
return [a / length, b / length]
return [a, b]
def perp2d(a, b):
return [-b, a]
def rotate2d(x, y, rads):
cos = math.cos(rads)
sin = math.sin(rads)
return [(x * cos) - (y * sin), (x * sin) + (y * cos)]
def distance2d(x1, y1, x2, y2):
x = x1 - x2
y = y1 - y2
return math.sqrt(x*x + y*y)
def toRadians(x, y):
v = normalize(x, y)
return math.atan2(v[1], v[0])
def toVector(rads):
return [math.cos(rads), math.sin(rads)]
def intersection2d(splitterStart, splitterEnd, lineStart, lineEnd):
s1 = splitterStart
e1 = splitterEnd
s2 = lineStart
e2 = lineEnd
a1 = e1[1] - s1[1]
b1 = s1[0] - e1[0]
c1 = a1 * s1[0] + b1 * s1[1]
a2 = e2[1] - s2[1]
b2 = s2[0] - e2[0]
c2 = a2 * s2[0] + b2 * s2[1]
delta = a1 * b2 - a2 * b1
# if lines are parallel, the result will be delta = 0
if delta != 0:
return [(b2 * c1 - b1 * c2) / delta, (a1 * c2 - a2 * c1) / delta]
return None