Bresenham's Line Algorithm
The Bresenham line algorithm is an algorithm which determines which order to form a close approximation to a straight line between two given points. It is commonly used to draw lines on a computer screen, as it uses only integer addition, subtraction and bit shifting, all of which are very cheap operations in standard computer architectures. It is one of the earliest algorithms developed in the field of computer graphics. A minor extension to the original algorithm also deals with drawing circles.
While algorithms such as Wu's algorithm are also frequently used in modern computer graphics because they can support antialiasing, the speed and simplicity of Bresenham's line algorithm means that it is still important. The algorithm is used in hardware such as plotters and in the graphics chips of modern graphics cards. It can also be found in many software graphics libraries. Because the algorithm is very simple, it is often implemented in either the firmware or the graphics hardware of modern graphics cards.
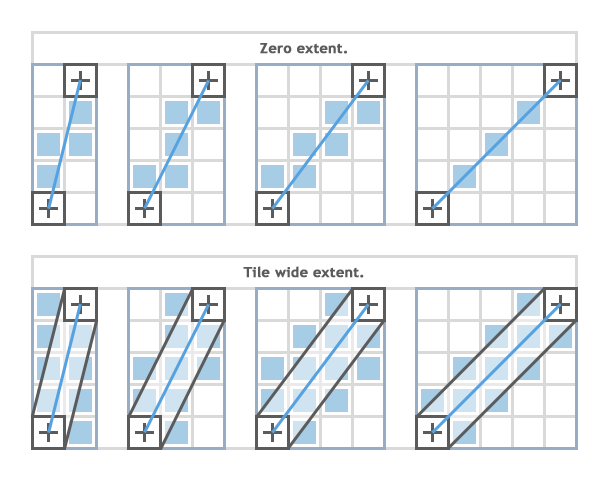
Raycasting Usage
Works great for raycasting for line of sight etc. and can be useful for pathfinding in tile based games.
Here is an example usage for Monstergeddon:
void MonsterTileMap::rayCast(int startX, int startY, int endX, int endY, std::function<void(MonsterTile*)> callback)
{
std::vector<sf::Vector2i> result = VectorHelper::BresenhamLine(startX, startY, endX, endY);
// (tileSize.y / 2) optimizes over 1 because we dont need to inspect every pixel point
for(int i=0; i < result.size(); i += (tileSize.y / 2))
{
MonsterTile* tile = getTileAtPosition(result[i].x, result[i].y);
callback(tile);
}
}C++ Implementation
Pulled from roguebasin. plot() draws a "dot" at (x, y):
#include <cstdlib>
void Bresenham(int x1,
int y1,
int const x2,
int const y2)
{
int delta_x(x2 - x1);
// if x1 == x2, then it does not matter what we set here
signed char const ix((delta_x > 0) - (delta_x < 0));
delta_x = std::abs(delta_x) << 1;
int delta_y(y2 - y1);
// if y1 == y2, then it does not matter what we set here
signed char const iy((delta_y > 0) - (delta_y < 0));
delta_y = std::abs(delta_y) << 1;
plot(x1, y1);
if (delta_x >= delta_y)
{
// error may go below zero
int error(delta_y - (delta_x >> 1));
while (x1 != x2)
{
if ((error >= 0) && (error || (ix > 0)))
{
error -= delta_x;
y1 += iy;
}
// else do nothing
error += delta_y;
x1 += ix;
plot(x1, y1);
}
}
else
{
// error may go below zero
int error(delta_x - (delta_y >> 1));
while (y1 != y2)
{
if ((error >= 0) && (error || (iy > 0)))
{
error -= delta_y;
x1 += ix;
}
// else do nothing
error += delta_x;
y1 += iy;
plot(x1, y1);
}
}
}